КВАДАР
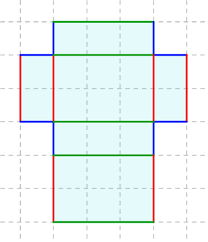
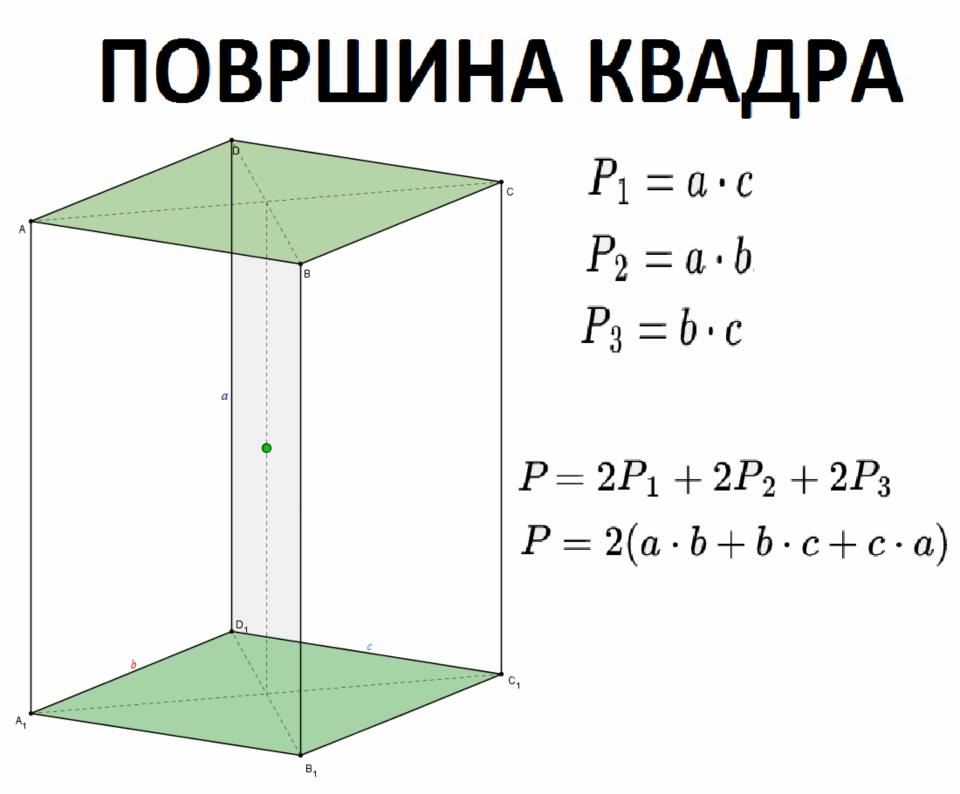
Квадар је рогљасто геометријско тело ограничено са шест правоугаоника.
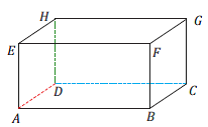
* Стране квадра: правоугаоници. Квадар има 6 страна. То су: ABFE, BCGF, CDGH, ADHE, EFGH, ABCD.
* Ивице квадра: странице правоугаоника. Квадар има 12 ивица. ( По четири ивице квадра су једнаке дужине. ) То су: AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, DH.
* Темена квадра: темена правоугаоника. Квадар има 8 темена. To су: A, B, C, D, F, G, E, H.
Два наспрамна правоугаоника квадра су подударна и паралелна.
Квадар је рогљасто геометријско тело ограничено са шест правоугаоника.
* Стране квадра: правоугаоници. Квадар има 6 страна. То су: ABFE, BCGF, CDGH, ADHE, EFGH, ABCD.
* Ивице квадра: странице правоугаоника. Квадар има 12 ивица. ( По четири ивице квадра су једнаке дужине. ) То су: AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, DH.
* Темена квадра: темена правоугаоника. Квадар има 8 темена. To су: A, B, C, D, F, G, E, H.
Два наспрамна правоугаоника квадра су подударна и паралелна.
КОЦКА
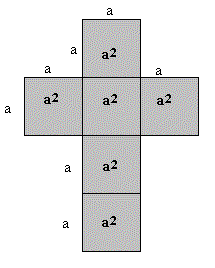
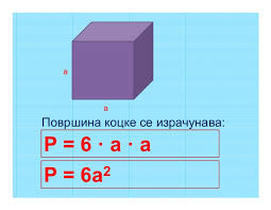
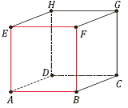
Коцка има 6 страна. Стране коцке су квадрати који су подударни.
Дужи које ограничавају те квадрате су ивице коцке и има их укупно 12. Оне су једнаке по дужини.
Крајње тачке ивица су темена коцке и има их укупно 8. Свако теме је заједничко за 3 ивице.
Две стране коцке које немају ниједну заједничку тачку су наспрамне странице.
Суседне странице коцке имају 2 заједничке тачке ( 2 заједничка темена).
* Коцка има:
– 6 страна ( математички запис)
– 8 темена
– 12 ивица
– наспрамне странице
– суседне странице
Коцка има 6 страна. Стране коцке су квадрати који су подударни.
Дужи које ограничавају те квадрате су ивице коцке и има их укупно 12. Оне су једнаке по дужини.
Крајње тачке ивица су темена коцке и има их укупно 8. Свако теме је заједничко за 3 ивице.
Две стране коцке које немају ниједну заједничку тачку су наспрамне странице.
Суседне странице коцке имају 2 заједничке тачке ( 2 заједничка темена).
* Коцка има:
– 6 страна ( математички запис)
– 8 темена
– 12 ивица
– наспрамне странице
– суседне странице
Множење збира и разлике
1. Круговима су приказане кованице од 10 дин. и 5 дин. Колико укупно има новца?
(10 + 5) • 4 = 10 • 4 + 5 • 4 (20 – 5) • 4 = 20 • 4 –5 • 4
(a + b) • c = a • с + b • c (a – b ) • c = a • c – b • c
Збир множимо неким бројем тако што сваки сабирак помножимо тим бројем, па добијене производе саберемо.
Разлику множимо неким бројем тако што и умањеник и умањилац помножимо тим бројем , па добијене производе одузмемо.
* Множимо број на два начина:
а) 107 ∙ 8
107 ∙ 8 = ( 100 + 7 ) ∙ 8 = 100 ∙ 8 + 7 ∙ 8 = 800 + 56 = 856
107 ∙ 8 = ( 110 – 3 ) ∙ 8 = 110 ∙ 8 + 3 ∙ 8 = 880 – 24 = 856
б) 105 ∙ 18
105 ∙ 18 = 105 ∙ ( 10 + 8 ) = 105 ∙ 10 + 105 ∙ 8 = 1 050 + 840 = 1 890
105 ∙ 18 = 105 ∙ (20 – 2) = 105 ∙ 20 – 105 ∙ 2 = 2 100 – 210 = 1 890
* Множимо на лакши начин:
194 ∙ 55 = (200 – 6) ∙ 55 = 200 ∙ 55 – 6 ∙ 55 = 11 000 – 330 = 10 670
1 002 ∙ 67 = (1 000 + 2) ∙ 67 = 1 000 ∙ 67 + 2 ∙ 67 = 67 000 + 134 = 67 134
25 ∙ 19 = 25 ∙ ( 20 – 1 ) = 25 ∙ 20 – 25 ∙ 1 = 500 – 25 = 475
21 ∙ 16 + 79 ∙ 16 = ( 21 + 79 ) ∙ 16 = 100 ∙ 16 = 1 600
Дељење збира и разлике
1.Мама је двојици синова купила 4 плаве и 8 црвених лоптица. Како браћа могу подједнако да поделе лоптице?
Укупан број лоптица делимо на два дела.
( 4 + 8 ) : 2 = 12 : 2 = 6
Прво делимо плаве па црвене лоптице:
4 : 2 + 8 : 2 = 2 + 4 = 6
( 4 + 8 ) : 2 = 4 : 2 + 8 : 2
( а + b ) : c = a : c + b : c
* Када су сви сабирци дељиви неким бројем, тада је и њихов збир дељив тим бројем.
2. Троје деце деле 30 кликера, али 3 кликера су се изгубила. По колико кликера ће добити свако од њих?
( 30 – 3) : 3 = 27 : 3 = 9
( 30 – 3) : 3 = 30 : 3 – 3 : 3 = 10 – 1 = 9
( а – b ) : c = а : c – b : c
* Када су умањеник и умањилац дељиви неким бројем, онда је и њихова разлика дељива тим бројем.
* Делимо збир на два начина:
а) ( 60 + 21 ) : 3
( 60 + 21 ) : 3 = 60 : 3 + 21 : 3 = ______________________
( 60 + 21 ) : 3 = 91 : 3 = _____________________________
б) (600 + 400) : 10
( 600 + 400 ) : 10 = ________________________________
( 600 + 400 ) : 10 = ________________________________
* Делимо разлику на два начина:
а) (505 – 55) : 5
( 505 – 55 ) : 5 = 505 : 5 – 55 : 5 =______________________
( 505 – 55 ) : 5 = ___________________________________
б) ( 217 – 175 ) : 7
( 217 – 175 ) : 7 = ________________________________
( 217 – 175 ) : 7= ________________________________
1. Круговима су приказане кованице од 10 дин. и 5 дин. Колико укупно има новца?
(10 + 5) • 4 = 10 • 4 + 5 • 4 (20 – 5) • 4 = 20 • 4 –5 • 4
(a + b) • c = a • с + b • c (a – b ) • c = a • c – b • c
Збир множимо неким бројем тако што сваки сабирак помножимо тим бројем, па добијене производе саберемо.
Разлику множимо неким бројем тако што и умањеник и умањилац помножимо тим бројем , па добијене производе одузмемо.
* Множимо број на два начина:
а) 107 ∙ 8
107 ∙ 8 = ( 100 + 7 ) ∙ 8 = 100 ∙ 8 + 7 ∙ 8 = 800 + 56 = 856
107 ∙ 8 = ( 110 – 3 ) ∙ 8 = 110 ∙ 8 + 3 ∙ 8 = 880 – 24 = 856
б) 105 ∙ 18
105 ∙ 18 = 105 ∙ ( 10 + 8 ) = 105 ∙ 10 + 105 ∙ 8 = 1 050 + 840 = 1 890
105 ∙ 18 = 105 ∙ (20 – 2) = 105 ∙ 20 – 105 ∙ 2 = 2 100 – 210 = 1 890
* Множимо на лакши начин:
194 ∙ 55 = (200 – 6) ∙ 55 = 200 ∙ 55 – 6 ∙ 55 = 11 000 – 330 = 10 670
1 002 ∙ 67 = (1 000 + 2) ∙ 67 = 1 000 ∙ 67 + 2 ∙ 67 = 67 000 + 134 = 67 134
25 ∙ 19 = 25 ∙ ( 20 – 1 ) = 25 ∙ 20 – 25 ∙ 1 = 500 – 25 = 475
21 ∙ 16 + 79 ∙ 16 = ( 21 + 79 ) ∙ 16 = 100 ∙ 16 = 1 600
Дељење збира и разлике
1.Мама је двојици синова купила 4 плаве и 8 црвених лоптица. Како браћа могу подједнако да поделе лоптице?
Укупан број лоптица делимо на два дела.
( 4 + 8 ) : 2 = 12 : 2 = 6
Прво делимо плаве па црвене лоптице:
4 : 2 + 8 : 2 = 2 + 4 = 6
( 4 + 8 ) : 2 = 4 : 2 + 8 : 2
( а + b ) : c = a : c + b : c
* Када су сви сабирци дељиви неким бројем, тада је и њихов збир дељив тим бројем.
2. Троје деце деле 30 кликера, али 3 кликера су се изгубила. По колико кликера ће добити свако од њих?
( 30 – 3) : 3 = 27 : 3 = 9
( 30 – 3) : 3 = 30 : 3 – 3 : 3 = 10 – 1 = 9
( а – b ) : c = а : c – b : c
* Када су умањеник и умањилац дељиви неким бројем, онда је и њихова разлика дељива тим бројем.
* Делимо збир на два начина:
а) ( 60 + 21 ) : 3
( 60 + 21 ) : 3 = 60 : 3 + 21 : 3 = ______________________
( 60 + 21 ) : 3 = 91 : 3 = _____________________________
б) (600 + 400) : 10
( 600 + 400 ) : 10 = ________________________________
( 600 + 400 ) : 10 = ________________________________
* Делимо разлику на два начина:
а) (505 – 55) : 5
( 505 – 55 ) : 5 = 505 : 5 – 55 : 5 =______________________
( 505 – 55 ) : 5 = ___________________________________
б) ( 217 – 175 ) : 7
( 217 – 175 ) : 7 = ________________________________
( 217 – 175 ) : 7= ________________________________
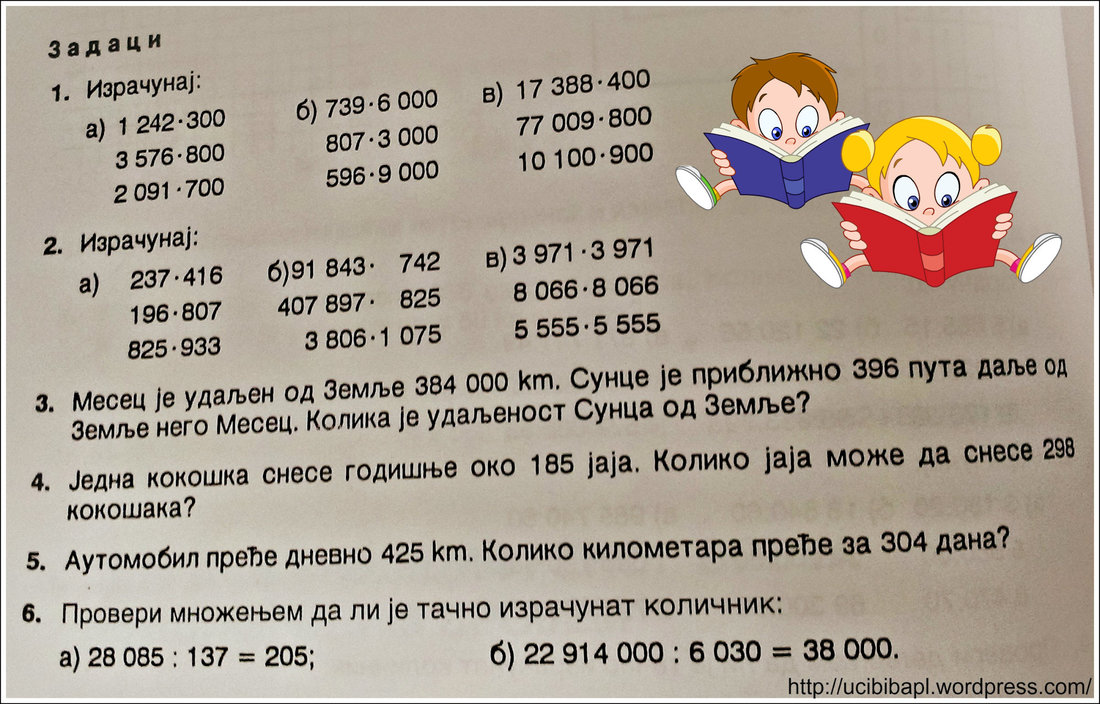
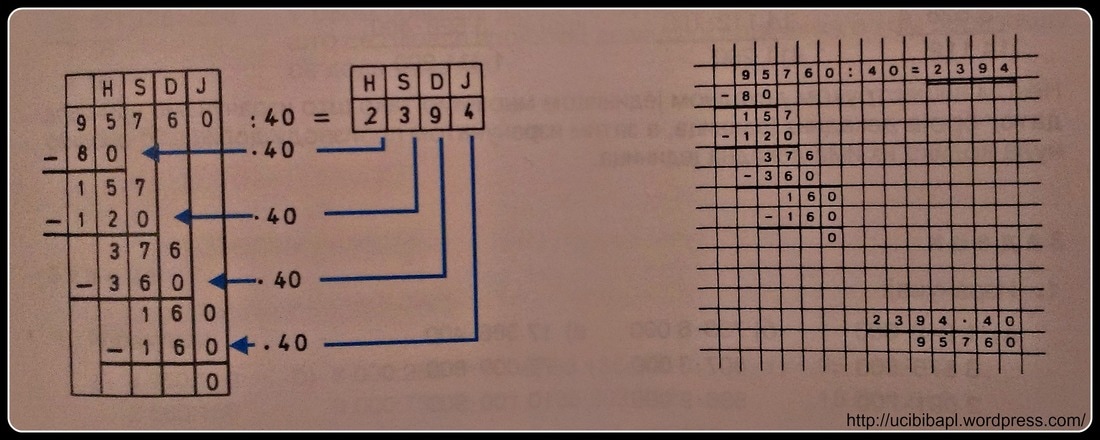
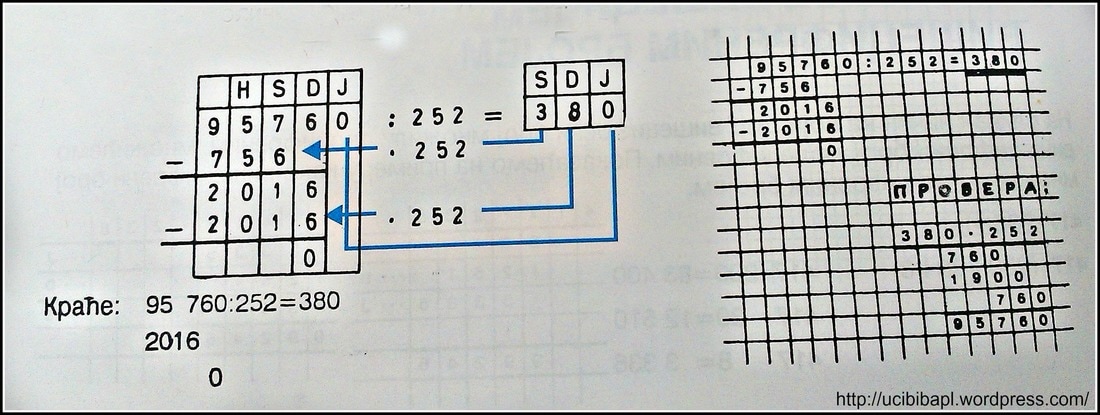
Дељење вишецифрених бројева
Множење вишецифреног броја једноцифреним.Обновити множење троцифрених бројева једноцифреним на следећим примерима:
1. Израчунај ти колико је 182 · 5.
Да би добио тачно решење препешачи цео свет.
Али ко је паметан, решиће ово тако,
хајде и ти си паметан, реши ово лако!
2. Једна девојчица Мила,
Има веома много стила.
Колико има пара,
Ако у 7 касица има по 446 динара?
3. У робној кући има 312 капута,
На којима се налази по 4 дугмета жута.
Колико у робној кући на 312 капута,
Има укупно дугмета жута?
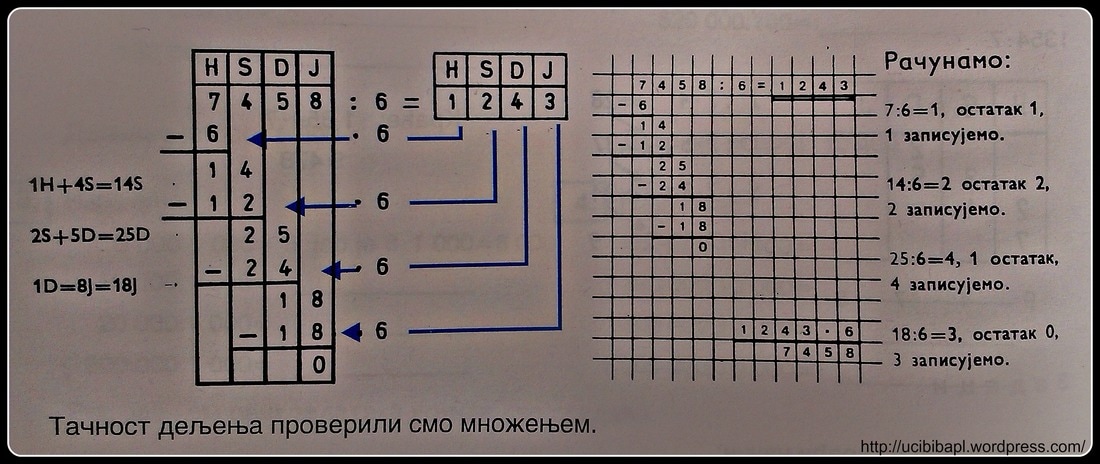
Објашњење множења вишецифреног броја једноцифреним:
Завод за уџбенике и наставна средства Београд
1. Израчунај ти колико је 182 · 5.
Да би добио тачно решење препешачи цео свет.
Али ко је паметан, решиће ово тако,
хајде и ти си паметан, реши ово лако!
2. Једна девојчица Мила,
Има веома много стила.
Колико има пара,
Ако у 7 касица има по 446 динара?
3. У робној кући има 312 капута,
На којима се налази по 4 дугмета жута.
Колико у робној кући на 312 капута,
Има укупно дугмета жута?
Објашњење множења вишецифреног броја једноцифреним:
Завод за уџбенике и наставна средства Београд
Уочавамо:
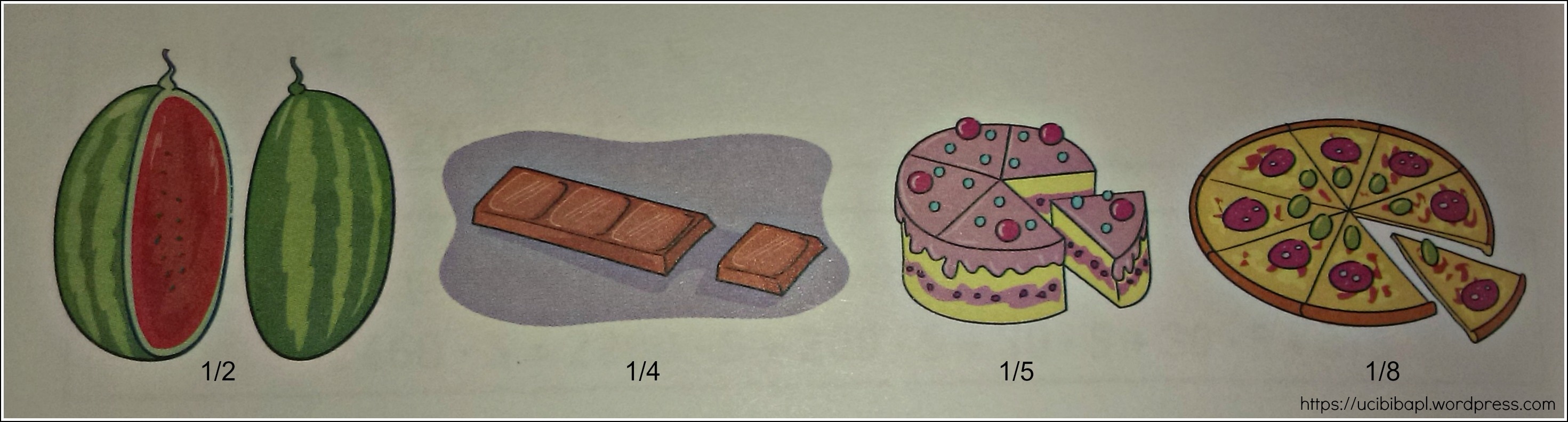
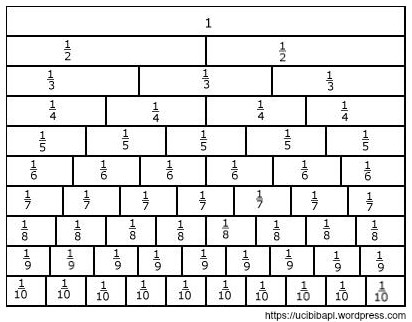
1 = 2/2 = 3/3 = 4/4 = 5/5 = 6/6 =7/7 = …
1/2 = 2/4 = 3/6 = 4/8 = 5/10 1/3 =2/6 =3/9
1/4 = 2/8 2/5 = 4/10
Такође уочавамо да је 1/2 >1/3 > 1/4 >1/5 > … , као што је и
2/9 > 2/8 > 2/7 > 2/6 >… и закључујемо: Када разломци имају исте бројиоце, већи је онај разломак чији је именилац мањи.
Уочавамо да је и: 1/8 < 2/8 < 3/8 < … , али и 2/5 < 3/5 < 4/5< … и закључујемо: Када разломци имају исте имениоце, већи је онај разломак чији је бројилац већи.
1 = 2/2 = 3/3 = 4/4 = 5/5 = 6/6 =7/7 = …
1/2 = 2/4 = 3/6 = 4/8 = 5/10 1/3 =2/6 =3/9
1/4 = 2/8 2/5 = 4/10
Такође уочавамо да је 1/2 >1/3 > 1/4 >1/5 > … , као што је и
2/9 > 2/8 > 2/7 > 2/6 >… и закључујемо: Када разломци имају исте бројиоце, већи је онај разломак чији је именилац мањи.
Уочавамо да је и: 1/8 < 2/8 < 3/8 < … , али и 2/5 < 3/5 < 4/5< … и закључујемо: Када разломци имају исте имениоце, већи је онај разломак чији је бројилац већи.